Перцентиль в excel
Примеры функции ПЕРСЕНТИЛЬ для расчета перцентиля в Excel
Функция ПЕРСЕНТИЛЬ в Excel предназначена для определения k-й доли перцентили для числовых значений исследуемого интервала и возвращает соответствующий результат.
Метод перцентилей в Excel по функции ПЕРСЕНТИЛЬ с примерами
Предположим, имеется вариационный ряд данных с минимальным и максимальным значениями, обозначаемых P0 и P100 соответственно. K-й перцентиль – это некоторое значение X из данного ряда, которое делит все имеющиеся в нем значения на две группы: K% значений, которые меньше X, и оставшиеся значения (то есть 1-K%), которые превышают X.
Для определения перцентилей необходимо:
- Отсортировать значения в исследуемом ряде данных в порядке возрастания.
- Найти некоторое значение в отсортированном ряде, для которого K% значений будут меньшими данного значения. При ручном расчете можно использовать формулу n*K%-1, где n – число элементов в исследуемом ряде значений.
- Определенное выше значение является K-й перцентилю по определению.
Функция ПЕРСЕНТИЛЬ считается устаревшей после выхода MS Office версии 2010 года, в которую были включены функции ПРОЦЕНТИЛЬ.ИСКЛ и ПРОЦЕНТИЛЬ.ВКЛ, которые в совокупности предлагают расширенный функционал для расчетов. Рассматриваемая функция была оставлена для совместимости с более старыми версиями табличного редактора.
Пример расчета перцентиля с использованием функции ПЕРСЕНТИЛЬ в Excel
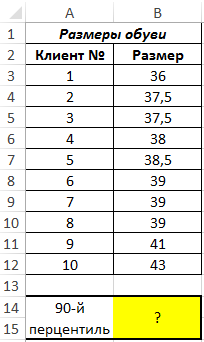
Пример 1. В магазин будет завезена новая партия обуви. Ранее в рамках маркетингового исследования были записаны размеры ног 10 случайных клиентов. На основании имеющихся данных определить размер обуви, являющийся пороговым значением для 90% клиентов.
Вид таблицы данных:
Для расчета используем функцию:
- B3:B12 – исследуемый ряд значений;
- 0,9 – число, указывающее, что необходим поиск 90-й перцентили (0,9=90%).
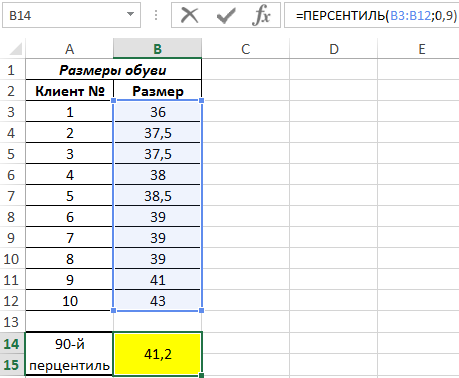
В результате вычислений формулы получен 90 перцентиль. Найденное значение не соответствует ни одному из рассматриваемого ряда, поскольку функция ПЕРСЕНТИЛЬ выполнила интерполяцию данных. 90% клиентов покупают обувь до 41 размера включительно.
Как рассчитать перцентиль в Excel с помощью функции ПЕРСЕНТИЛЬ
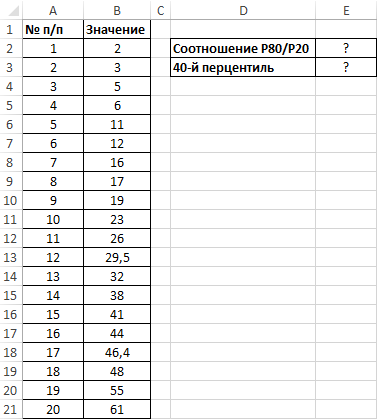
Пример 2. В таблице введен ряд некоторых значений. Необходимо:
- Определить, во сколько раз 80-й перцентиль превышает 20-й перцентиль.
- Рассчитать 40-й перцентиль без использования рассматриваемой функции.
Вид таблицы данных:
Для поиска значения соотношения используем следующую запись:
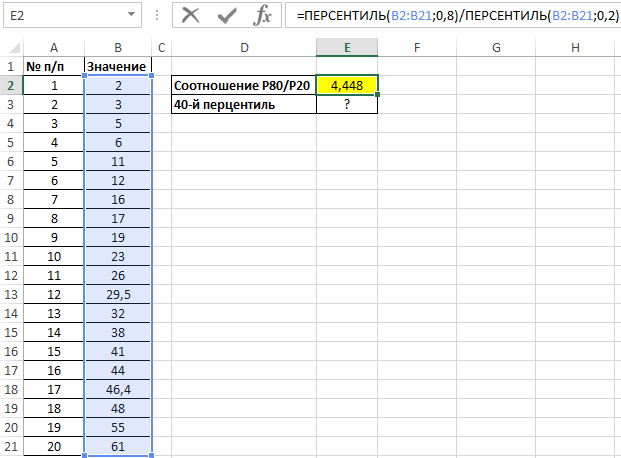
То есть, для исследуемого ряда значений 80-й перцентиль превышает 20-й почти в 4,5 раз.
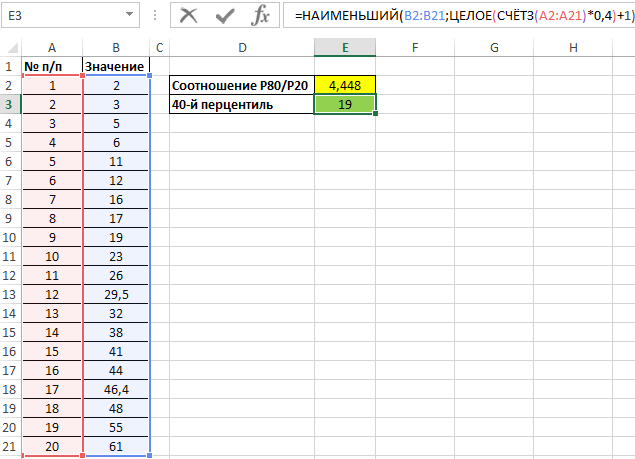
Альтернативный способ нахождения перцентиля – следующая формула:
Данная запись соответствует формуле, указанной в определении понятия перцентиль. Результат вычислений:
Рядом (справа) указано значение, полученное с использованием функции ПЕРСЕНТИЛЬ:
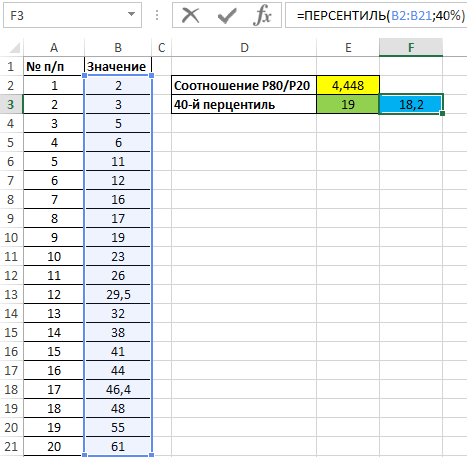
Значения отличаются, поскольку рассматриваемая функция выполняет интерполяцию данных.
Что такое функция ПЕРСЕНТИЛЬ и как с ней работать в Excel
Функция имеет следующий синтаксис:
- массив – обязательный для заполнения, принимает статический массив числовых данных или ссылку на диапазон ячеек с числами, для которых требуется вычислить значение k-го перцентиля;
- k – обязательный для заполнения, принимает числовые значения из диапазона от 0 до 1 (оба включительно), характеризующие номер перцентили для расчета (например, 0,25 – 25-я перцентиль, 0,5 – 50-я перцентиль).
- Перцентиль удобен для установления критериев отбора каких-либо данных. Например, на вступительных экзаменах почти все студенты не смогли преодолеть проходной порог (минимальное количество баллов для поступления в ВУЗ). Чтобы избежать недобора, можно ввести другой критерий – перцентиль, который поможет отобрать лучших абитуриентов на основании имеющихся данных о баллах за экзамены, а не установленных ранее критериев (проходного балла).
- Если исследуемый ряд (указан в виде аргумента массив) содержит нечисловые данные (текст, логические ИСТИНА или ЛОЖЬ, имена), функция исключает их из расчетов. Например, =ПЕРСЕНТИЛЬ(<1;4;5;7;11>;0,5) вернет значение 5, а =ПЕРСЕНТИЛЬ(<1;4;"е";7;11>;0,5) – 5,5.
- Функция возвращает код ошибки #ЗНАЧ!, если аргумент k указан в виде нечисловых данных (имя или текст, не преобразуемые в число). Нечисловые данные, преобразуемые к числам, являются допустимыми вариантами указания аргумента k . Например, =ПЕРСЕНТИЛЬ(<1;4;5;7;11>;”0,5”) вернет значение 5, =ПЕРСЕНТИЛЬ(<1;4;5;7;11>;ИСТИНА) – 11.
- Рассматриваемая функция генерирует код ошибки #ЧИСЛО!, если аргумент k задан в виде числа не из диапазона допустимых значений, то есть >1 или k , не кратных 1/(n-1), функция интерполирует данные для расчетов (n – число элементов массива).
Процентили
— это характеристики набора данных, которые выражают ранги элементов массива в виде чисел от 1 до 100, и являются показателем того, какой процент значений находится ниже определенного уровня.
Например, значение 30-й процентили указывает, что 30% значений располагается ниже этого уровня.
На конкретном примере поясним понятие процентиля:
Пример 1 . Группа студентов из 20 человек получила на экзамене по статистике следующие балы: три студента — 5 баллов, 8 студентов — 4 балла, 6 студентов — 3 бала и 3 студента — 2 балла. Вычислить процентиль успеваемости каждого студента.
Решение.
Формула процентиля
Процентиль = n(x≤X)/N*100
n(x≤X) — число студентов, получивших бал не менее X ,
X — количество балов конкретного студента, процентиль которого находим ,
N — число всех студентов .
Для удобства вычислений ранжируем выборку балов от максимального значения до минимального ( в порядке убывания): 5,5,5,4,4,4,4,4,4,4,4,3,3,3,3,3,3,2,2,2
Допустим нам необходимо определить процентиль студента Иванова получившего на экзамене 5 баллов:
Находим n(x≤X)=n(x≤5)=20 — т.е. 20 студентов получили бал не выше 5, тода
Процентиль (Иванова) = 20/20*100=100
Допустим необходимо определить процентиль студента Петрова получившего на экзамене 4 балла:
Находим n(x≤X)=n(x≤4)=17 — т.е. 17 студентов получили бал не выше 4, тода
Процентиль (Петрова) = 17/20*100=85
Допустим необходимо определить процентиль студента Сидорова получившего на экзамене 3 балла:
Находим n(x≤X)=n(x≤3)=9 — т.е. 9 студентов получили бал не выше 3, тода
Процентиль (Иванова) = 9/20*100=45
После расчета процентиля можно составить таблицу стандартизации. Для наших баллов она будет выглядеть следующим образом:
| Бал | Процентили |
| 5 | 100 |
| 4 | 85 |
| 3 | 45 |
| 2 | 15 |
Алгоритм расчета процентилей
1. Для каждого человека посчитать, какое количество человек набрало столько же или меньше баллов.
2. Посчитать сколько процентов составляет это количество от всей выборки.
Процентиль – это процент людей из выборки, набравших столько же или меньше баллов, чем конкретный человек.
Процентиль является достаточно распространенной шкалой стандартизации, среди психологов, социологов, биологов, медиков и т.д., т.к. очень удобен и понятен. Его диапазон от 1 до 100.
Процентили указывают на относительное положение индивида в выборке стандартизации. Их также можно рассматривать, как ранговые градации, общее число которых равно 100, с той лишь разницей, что при ранжировании принято начинать отсчет сверху, т.е. с лучшего члена группы, получающего ранг 1. В случае же процентилей отсчет ведется снизу, поэтому, чем ниже процентиль, тем хуже позиция индивида.
Процентиль может использоваться для стандартизации как нормально распределенных случайных величин СВ, так и данных с ненормальным распределением.
Расчет процентилей в Excel
Для расчета процентилей нам понадобится функция СЧЕТЕСЛИ.
Для расчета, для каждого значения нужно ввести формулу:
=(СЧЁТЕСЛИ(диапазон;условие)*100)/N , где N – количество человек.
Перцентили
Заметим, что перцентиль представляет собой какой-то элемент массива, имеющий определенный ранг и выраженный в тех же единицах, что и сам массив в целом. Так, 60-й перцентиль эффективности сбора металлолома в конторе «Ржавая подкова» составляет, скажем, 85062 руб. (измерен не в процентах, а в рублях, как элемент набора данных). Если этот 60-й перцен- тиль, равный 85062 руб., характеризует деятельность определенного агента по заготовкам (например, г-на Пупкина), то это означает, что примерно 60 % других тружеников имеют результат ниже, чем у г-на Пупкина, а 40 % — более высокие показатели.
Перцентили используются для двух целей:
чтобы показать значение элемента в массиве при заданном перцен- тильном ранге (например, «10-й перцентиль равен 46293 руб.»);
чтобы показать перцентильный ранг значения данного элемента в рассматриваемом массиве статистических данных (например, «эффективность заготовок металлолома агента г-на Козлевича составляет 65994 руб., что соответствует 55-му перцентилю»).
Продолжим рассмотрение нашей задачи. В диалоговом окне Ранг и персентиль заполним поле Входной интервал (рис.7).
Рис. 7. Диалоговое окно Ранг и перцентиль
В нем укажем данные 2-й графы табл. 3 (вместе с заголовком), относящиеся к фирме «Колокольный звон» (это диапазон ячеек $B$1:$B$13). Отметим флажком позицию Метки в первой строке (поскольку нам нужно со-хранить заголовок этой графы), а затем в окне Выходной интервал укажем ячейку $I$1, в которой будет размещена таблица с рассчитанными показателями рангов и перцентилей. После этого — кнопка ОК.
Затем аналогичным образом поступим с данными 3-й графы (сведения от фирмы «Мельхиор»). При заполнении диалогового окна Ранг и персентиль отметим диапазон ячеек $С$1:$С$13, а для опции Выходной интервал покажем ячейку, которая должна быть по соседству с первой половинкой нашей общей таблицы. Это ячейка $М$1.
В окончательном виде наша таблица примет следующий вид (рис.8).
Как видно, Excel аккуратно проранжировал результаты по каждому эпизоду, расположив студентов по местам в соответствии с их материальны- ми успехами, а также указал их перцентильный ранг (в %). Для дальнейших рассуждений данные по перцентилям мы использовать не станем, а вот ранги окажутся совершенно необходимыми. 1 J К L М N 0 Р Точка Фирма «Колокольный звон» Ранг Процент Точка Фирма «Мельхиор» Ранг Процент 11 3,5 1 100,00% 12 4,5 1 100,00% 12 3,4 2 90,90% 4 4,1 2 90,90% 6 3,3 3 81,80% 1 3,3 3 81,80% 4 3,2 4 72,70% 9 3,2 4 72,70% 2 3,1 5 63,60% 11 3,1 5 63,60% 1 2,8 6 54,50% 2 3 6 54,50% 9 2,5 7 45,40% 3 2,8 7 45,40% 5 2,4 8 36,30% 6 2,7 8 36,30% 10 2,3 9 27,20% 10 2,6 9 27,20% 7 2,2 10 18,10% 7 2,5 10 18,10% 3 2 11 9,00% 8 2,3 11 9,00% 8 1,8 12 ,00% 5 2,1 12 ,00% Рис. 8. Расчетная таблица с показателями рангов и перцентилей
На основании ранговых оценок организуем сводную таблицу, аналогичную уже знакомой нам табл.3 (рис.9). Для удобства перейдем на другой рабочий лист (Лист 2). Для выполнения последующих расчетов используем итоговый результат, отражающий сумму разностей квадратов рангов, равную 105. Оформим вспомогательную таблицу (рис.9), в которой укажем значение ScF = 105, размер выборки n = 12, а также предусмотрим в ней ячейку, где поместим рассчитанное значение коэффициента ранговой корреляции р (ячейка Е22).
Поместим курсор в ячейку Е22, а затем в поле формулы запишем уравнение, по которому будем рассчитать коэффициент р. Выглядит оно так:
= 1 — 6*(Е20)/(Е21*(Е21А2 — 1)) В ячейке появится искомый результат 0,632867. С округлением принимаем его равным 0,633 — коэффициент оказался именно таким, каким мы его вычислили «вручную».
Полученный результат показывает, что в данной ситуации надлежит высказать совершенно те же соображения по поводу исследуемого процесса, какие были сделаны для случая расчета коэффициента р традиционным способом. При доверительной вероятности 0,95 студенты вполне могут горделиво полагать, что их материальные достижения всецело определяются личным усердием и не зависят от каких-то иных привходящих факторов. Однако требование более строгой оценки (с вероятностью 99 %) делает такое мнение менее очевидным и для значимого статистического вывода возникает необходимость расширить выборку (привлечь для анализа большее число студентов) либо (при невозможности это сделать) отнестись к результату вполне философски.
Перцентиль: Альтернативный взгляд на данные
Сегодня поделюсь переводом интересной статьи от лондонского аналога нашего qRUG, QlikDevGroup.
Введение
Из этой статьи вы узнаете, как создать выражения для расчета распределения по перцентилям по вашему набору данных. Т.е., если сказать проще, такой график:
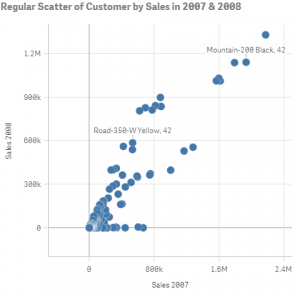
Вы сможете превратить в нечто подобное:
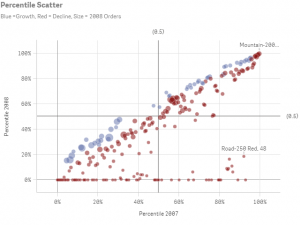
Перцентиль – это способ посмотреть на ваши данные в отношении ко всем другим значениям набора данных. Например, если вы хотите определить 10% самых активных покупателей за прошлый месяц, по сути, вы хотите увидеть всех покупателей выше границы в 90%.
Основная причина использования распределения по перцентилям – слишком плотное распределение данных. Например, на графике выше вы видите, как большинство точек в пузырьковой диаграмме сосредоточено внизу.
Таким образом, для того, чтобы понять распределение данных нам нужно увеличить график, при этом мы потерям полную картину данных и связей между ними. По этой причине предлагаю воспользоваться альтернативным способом представления данных – по перцентилю.
Проблемы при работе по средним:
- Средние скрывают выбросы и вы их не видите.
- Выбросы смещают средние значения, так что в системе, в которой существуют выбросы, средние значения уже не отражают нормальное состояние системы.
Выход из этой ситуации – перцентили.
НА ЗАМЕТКУ! Перцентили (квантили — в более широком представлении) часто превозносятся как средство преодоления фундаментального недостатка средних значений. Однако не стоит забывать, что перцентиль — это всего лишь число, так же как и среднее. Среднее отображает центр масс выборки, а перцентиль же показывает отметку верхнего уровня указанной доли выборки.
Фрактальный подход
В QlikView и QlikSense достаточно просто рассчитываются перцентили. Функция FRACTILE() будет показывать соответствующее значение перцентиля.
Так, для того чтобы найти ТОП 10% ваших клиентов (то есть тех, которые выше границы 90%), вам нужно использовать следующее выражение:
Такая формула отлично срабатывает для любой готовой меры , которая у нас есть. Но, как правило, требуется задать перцентиль для конкретного измерения, и в этом случае нужно использовать функцию FRACTILE вместе с функцией AGGR.
Например, если вы хотите показать перцентиль 90% по продажам ваших продуктов, то вам нужно использовать следующее выражение:
Подход ранжирования
Фрактальный подход отлично подходит для отображения значений перцентиля. Но для того, чтобы показать значения нескольких процентилей в одно и то же время, нужно использовать функцию RANK(), которая будет распределять данные по группам с одинаковыми значениями.
Например, если у нас есть следующий набор данных:
Применив RANK (), получим ранжирование в виде:
где группа 1-5 – отранжированные ТОП-5 значений.
Второй режим функции ранжирования возвращает значение DUAL.
В примере выше Qlik хранит группу 1-5 как двоичное значение (‘1-5’,1.5)
На следующем шаге следует взять нумерическую часть значений ранжирования и разделить ее на общее число уникальных значений в наборе данных. Так, мы увидим процентные значение, но наименьшие значения (те, которые имеют высший рейтинг), будут отражаться как топовые. Ну а дальше самым простым способом будет минусовать значения этого процента, чтобы инвертировать значения.
Так, если мы продолжим пример с продажами, выражение примет вид:
Эта функция – рабочая, но с некоторыми ограничениями:
- Функция хорошо работает по всему набору данных, только если не используются фильтры данных. Чтобы убрать это ограничение, нужно использовать Set Analysis.
- Выражение расценивает NULL продажи как правомерные значения данных, тем самым искажая результаты. Чтобы избавиться от этой проблемы, делаем проверку на NULL и заменяем их нулями.
В итоге получаем улучшенную формулу:
Практический пример:
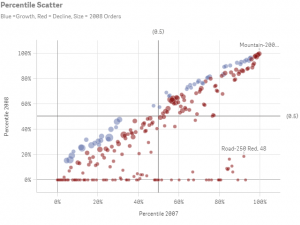
Далее рассмотрим пример создания диаграммы с процентилями для QlikSense 2.0.7
Диаграмма представляет продажу по каждому продукту в сравнении с процентильным ранжированием в 2007 и 2008 годах, а также объемом продаж в 2008. Также на графике выделены продукты, которые выросли и упали в перцентилях.
В жизни все не так просто, поэтому добавим немного сложностей и в тестовый пример J Некоторые продукты в 2008 не продавались, поэтому нам придется добавить дополнительную проверку на NULL значения продаж в случае применения фильтров.
Выражение для перцентиля 2007 года получается таким:
А для 2008 – таким:
Выражение для вычисления размера пузырьков:
И в завершении выражение для цветов диаграммы:
И в заключение я добавил дополнительные линии от 50% на обоих осях:
Заключение
Распределение по перцентилю помогает выявить паттерны между данными, которые могут быть скрыты при нормальном распределении. Рекомендую использовать анализ по перцентилям совместно с реальными объемами, чтобы посмотреть на данные с разных точек зрения.