Интервальный прогноз в excel

Создание прогноза в Excel для Windows

Если у вас есть статистические данные с зависимостью от времени, вы можете создать прогноз на их основе. При этом в Excel создается новый лист с таблицей, содержащей статистические и предсказанные значения, и диаграммой, на которой они отражены. С помощью прогноза вы можете предсказывать такие показатели, как будущий объем продаж, потребность в складских запасах или потребительские тенденции.

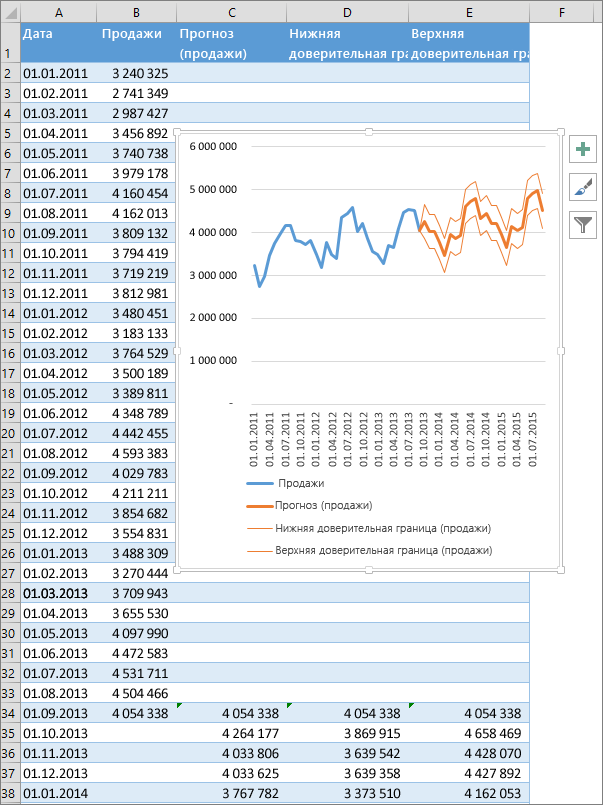
Создание прогноза

На листе введите два ряда данных, которые соответствуют друг другу:

ряд значений даты или времени для временной шкалы;

ряд соответствующих значений показателя.

Эти значения будут предсказаны для дат в будущем.

Примечание: Для временной шкалы требуются одинаковые интервалы между точками данных. Например, это могут быть месячные интервалы со значениями на первое число каждого месяца, годичные или числовые интервалы. Если на временной шкале не хватает до 30 % точек данных или есть несколько чисел с одной и той же меткой времени, это нормально. Прогноз все равно будет точным. Но для повышения точности прогноза желательно перед его созданием обобщить данные.

Выделите оба ряда данных.

Совет: Если выделить ячейку в одном из рядов, Excel автоматически выделит остальные данные.

На вкладке Данные в группе Прогноз нажмите кнопку Лист прогноза.

В окне Создание листа прогноза выберите график или гистограмму для визуального представления прогноза.

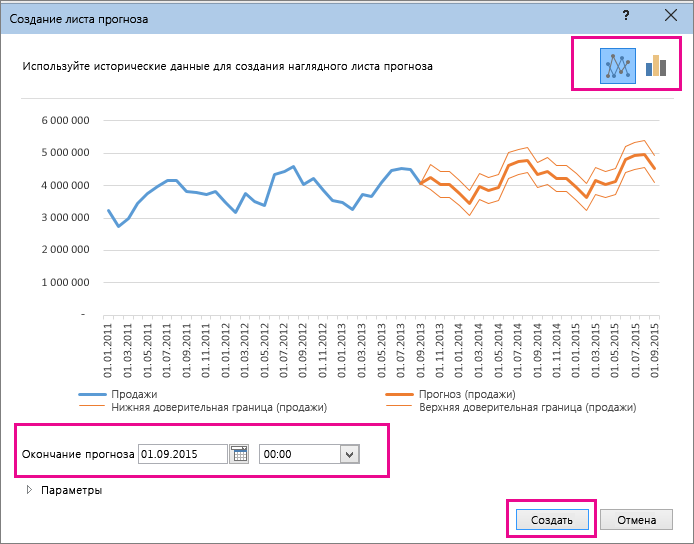
В поле Завершение прогноза выберите дату окончания, а затем нажмите кнопку Создать.

В Excel будет создан новый лист с таблицей, содержащей статистические и предсказанные значения, и диаграммой, на которой они отражены.

Этот лист будет находиться слева от листа, на котором вы ввели ряды данных (то есть перед ним).

Настройка прогноза

Если вы хотите изменить дополнительные параметры прогноза, нажмите кнопку Параметры.

Здесь вы найдете сведения о каждом из вариантов в приведенной ниже таблице.

Выберите дату, с которой должен начинаться прогноз. При выборе даты начала, которая наступает раньше, чем заканчиваются статистические данные, для построения прогноза используются только данные, предшествующие ей (это называется «ретроспективным прогнозированием»).

Если вы задаете прогноз до последней исторической точки, вы сможете оценить точность прогноза, так как вы можете сравнить прогнозируемые ряды с фактическими данными. Но если начать прогнозирование со слишком ранней даты, построенный прогноз может отличаться от созданного на основе всех статистических данных. При использовании всех статистических данных прогноз будет более точным.

Если в ваших данных прослеживаются сезонные тенденции, то рекомендуется начинать прогнозирование с даты, предшествующей последней точке статистических данных.

Установите или снимите флажок Доверительный интервал, чтобы показать или скрыть его. Доверительный интервал — это диапазон вокруг каждого предсказанного значения, в который в соответствии с прогнозом (при нормальном распределении) предположительно должны попасть 95 % точек, относящихся к будущему. Доверительный интервал помогает определить точность прогноза. Чем он меньше, тем выше достоверность прогноза для данной точки. Доверительный интервал по умолчанию определяется для 95 % точек, но это значение можно изменить с помощью стрелок вверх или вниз.

Сезонность является числом для длины (количеством очков) шаблона сезонов и автоматически определяется. Например, в ежегодном цикле продаж с каждой точкой, представляющей месяц, сезонность составляет 12. Вы можете переопределить автоматическое обнаружение, выбрав параметр вручную , а затем выбрав номер.

Примечание: Если вы хотите задать сезонность вручную, не используйте значения, которые меньше двух циклов статистических данных. При таких значениях этого параметра приложению Excel не удастся определить сезонные компоненты. Если же сезонные колебания недостаточно велики и алгоритму не удается их выявить, прогноз примет вид линейного тренда.

Диапазон временной шкалы

Здесь можно изменить диапазон, используемый для временной шкалы. Этот диапазон должен соответствовать параметру Диапазон значений.

Здесь можно изменить диапазон, используемый для рядов значений. Этот диапазон должен совпадать со значением параметра Диапазон временной шкалы.

Заполнить отсутствующие точки с помощью

Для обработки отсутствующих точек в Excel используется интерполяция, что означает, что пропущенная точка будет выполнена как взвешенное среднее арифметическое соседних точек, пока не пройдет менее 30% точек. Чтобы вместо отсутствующих точек обрабатывались нули, в списке выберите ноль .

Объединение дубликатов с помощью

Если данные содержат несколько значений с одной меткой времени, Excel находит их среднее. Чтобы использовать другой метод вычисления (например, медиана или счёт), выберите нужный вариант вычисления из списка.

Включить статистические данные прогноза

Установите этот флажок, если хотите поместить на новом листе дополнительную статистическую информацию о прогнозе. При этом добавляется таблица статистики, созданной с помощью прогноза. ETS. STAT и включает в себя меры, например коэффициент сглаживания (альфа, бета, гамма) и метрики ошибок (Масе, смапе, мае, рмсе).

Формулы, используемые при прогнозировании

При использовании формулы для создания прогноза возвращаются таблица со статистическими и предсказанными данными и диаграмма. Прогноз предсказывает будущие значения на основе имеющихся данных, зависящих от времени, и алгоритма экспоненциального сглаживания (ETS) версии AAA.

Таблицы могут содержать следующие столбцы, три из которых являются вычисляемыми:

столбец статистических значений времени (ваш ряд данных, содержащий значения времени);

столбец статистических значений (ряд данных, содержащий соответствующие значения);

столбец прогнозируемых значений (вычисленных с помощью функции ПРЕДСКАЗ.ЕTS);

два столбца, представляющие доверительный интервал (вычисленные с помощью функции ПРЕДСКАЗ.ЕTS.ДОВИНТЕРВАЛ). Эти столбцы отображаются только в том случае, если в разделе » Параметры » установлен флажок » доверительный интервал «.

Скачайте пример книги.

Дополнительные сведения

Вы всегда можете задать вопрос специалисту Excel Tech Community, попросить помощи в сообществе Answers community, а также предложить новую функцию или улучшение на веб-сайте Excel User Voice.

См. также:

Примечание: Эта страница переведена автоматически, поэтому ее текст может содержать неточности и грамматические ошибки. Для нас важно, чтобы эта статья была вам полезна. Была ли информация полезной? Для удобства также приводим ссылку на оригинал (на английском языке).

Решение. Построение точечного и интервального прогнозов

Лабораторная работа №4

Построение точечного и интервального прогнозов.

Задача

По следующему временному ряду (табл. 1.) составить точечный и интервальный прогноз на 2012 г. с доверительной вероятностью Р=0,95.

Решение

1. По исходным данным строим точечную диаграмму (рис.1).

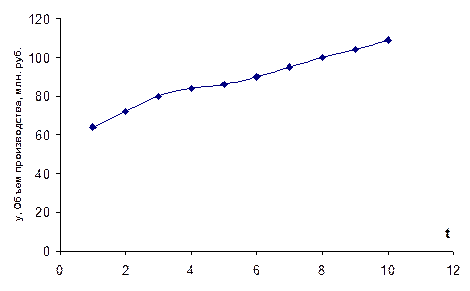
Рис. 1. Диаграмма, построенная по данным табл.1.

По характеру диаграммы ясно, что в качестве тренда можно использовать прямую.

2. Выводим на диаграмму линию и уравнение тренда (рис.2).

Для вывода линии и уравнения тренда навести курсор на график, щелкнуть правой кнопкой мыши, выбрать Добавить линию тренда, выбрать тип Линейная, поставить галочки для вывода уравнения на графике и вывода величины достоверности аппроксимации R^2.

Для выбора наиболее адекватного вида уравнения тренда используются и другие критерии. В программе Excel в качестве критерия адекватности математических функций, или, используя терминологию, принятую в Excel, величины достоверности аппроксимации, используется коэффициент детерминации R 2 , который вычисляется как отношение факторной дисперсии к общей дисперсии, т.е.

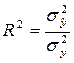
Если выбор вида тренда осуществляется с помощью критерия 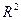, то выбирается тот тип трендового уравнения, для которого ве­личина 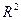наибольшая.

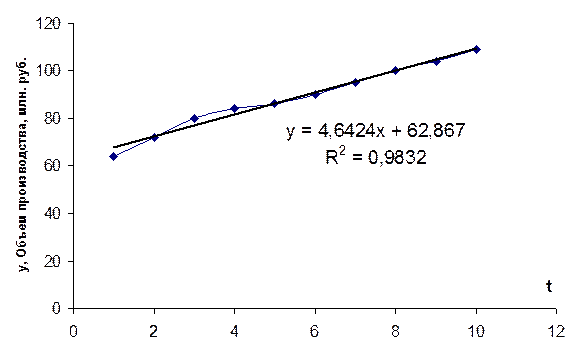
Рис. 2. Линия тренда и ее параметры, выведенные на диаграмму исходных значений

3. В столбце С (рис.3) рассчитываем уровни ряда на основании уравнения тренда: y=4,6424t+62,876.

Затем рассчитываем по формуле

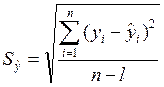
величину 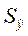и t_α на основании обратного распределения Стьюдента, чтобы получить доверительный интервал прогноза по формуле

.

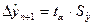4. В столбце D рассчитываем квадрат разности между исходными и расчетными значениями уровней временного ряда.

5. В ячейке D14 рассчитана сумма квадратов разности – 30,35.(графа 4). В ячейке D15 делим сумму на n-l=8, так как в данном примере число уровней ряда равно 10, а параметров в уравнении прямой – 2. Это число 3,79. В ячейке D16 — квадратный корень предыдущего числа – 1,95. Это и есть величина 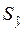. В ячейке D17 на основании функции F(x)= СТЬЮДРАСПОБР(0,05; 9) подсчитана величина t_α=2,26. И в ячейке D18 вычислено произведение 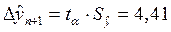. Это доверительный интервал прогноза (рис. 3).

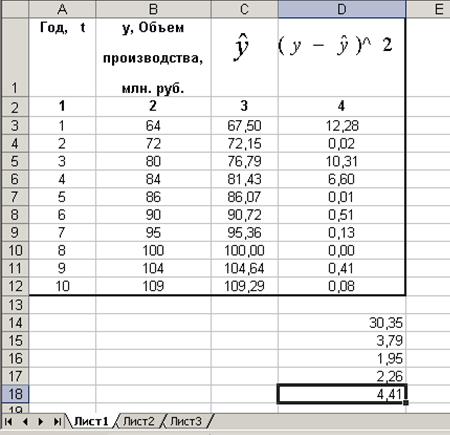
Рис. 3. Расчет доверительного интервала прогноза

6. Находим точечное значение прогноза по линии тренда (рис.4). Для этого в ячейку A13 добавляем новый момент времени t=t(11) (соответствующий 2012г.), и в ячейке С13 автоматически появляется значение линии тренда при t=t(11) – это число 113,93. Теперь для получения интервального прогноза из точечного прогноза нужно вычесть и прибавить величину 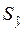· t_α=4,41. Таким образом, получаем доверительный интервал прогноза на 2012 год: [118,33; 109,52] (рис. 4).

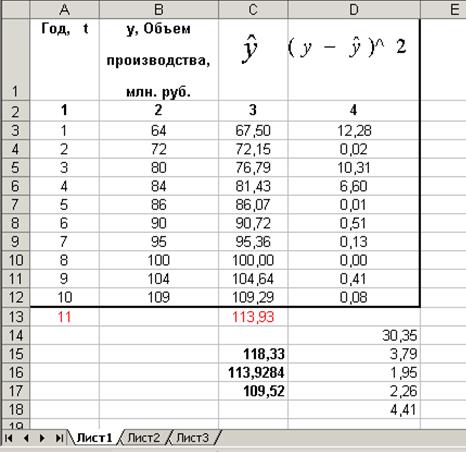
Рис. 4. Расчет точечного прогноза и его доверительного интервала

На основании построенной модели временного ряда можно производить интерполяцию в том случае, когда нужно восстановить значения внутри ряда. Например, объем производства в 2006 году неизвестен. Этот год соответствует моменту времени t=5. Для этого достаточно найти значение лини тренда от момента времени t=5 и подставить в исходный ряд недостающее значение (рис. 5).

Рис. 5. Интерполяция данных на основании уравнения тренда

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Да какие ж вы математики, если запаролиться нормально не можете. 8827 — | 7636 — или читать все.

Прогнозирование продаж в Excel с учетом сезонности

В прошлой статье мы уже разобрали, что такое временной ряд и функцию тренда. Теперь подробнее разберемся с терминологией и остановимся на одной из моделей временного ряда.

Из чего состоит временной ряд

Уровни временного ряда (Yt) представляют из себя сумму двух компонент:

1. Регулярную составляющую
2. Случайную составляющую

В свою очередь регулярная составляющая состоит из:

1. Тренда
2. Сезонности
3. Циклической составляющей

Однако, в модели необязательно наличие всех этих компонент сразу.

Случайная компонента отражает влияние случайных возмущений на модель, которые по отдельности имеют незначительное воздействие, но суммарно их влияние ощущается.

То есть, в общем случае временной ряд представляет из себя наличие четырех составляющих:

1. Тренд (Tt)
2. Сезонность (St)
3. Цикличность (Ct)
4. Случайные возмущения (Et)

Циклическая компонента, по сравнению с сезонностью, имеет более длительный эффект и меняется от цикла к циклу. Поэтому, ее обычно объединяют с трендом.

Виды моделей временного ряда

Обычно, выделяют две модели временного ряда и третью — смешанную.

Аддитивная модель

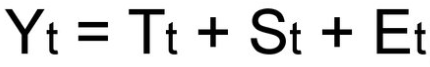
Мультипликативная модель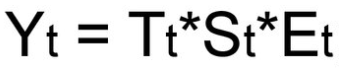

Смешанная модель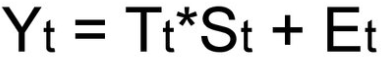

При выборе необходимой модели временного ряда смотрят на амплитуду колебаний сезонной составляющей. Если ее колебания относительно постоянны, то выбирают аддитивную модель. То есть, амплитуда колебаний примерно одинакова:

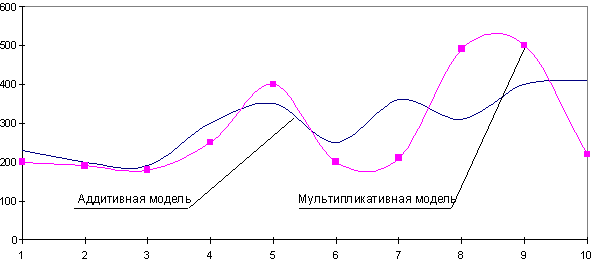
Если амплитуда сезонных колебаний возрастает или уменьшается, строят мультипликативную модель временного ряда, которая ставит уровни ряда в зависимость от значений сезонной компоненты.

Построение этих моделей сводится к расчету тренда (Tt), сезонности (St) и случайных возмущений (Et) для каждого уровня ряда (Yt).

Алгоритм построения модели

1. Выравниваем ряд с помощью скользящей средней, то есть сглаживаем ряд и отфильтровываем высокочастотные колебания.
2. Рассчитываем значение сезонной компоненты St.
3. Рассчитываем значения Tt с использованием полученного уравнения тренда.
4. Используя полученные значения St и Tt, находим прогнозные значения уровней временного ряда.
5. Оцениваем качество модели.

Реализация на практике

Итак, мы имеем на руках данные о продажах за 2016 и 2017 год и хотим спрогнозировать продажи на 2018 год.

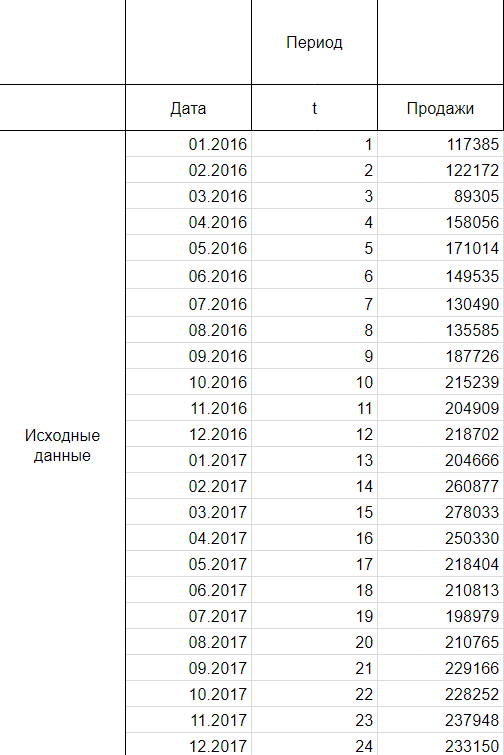
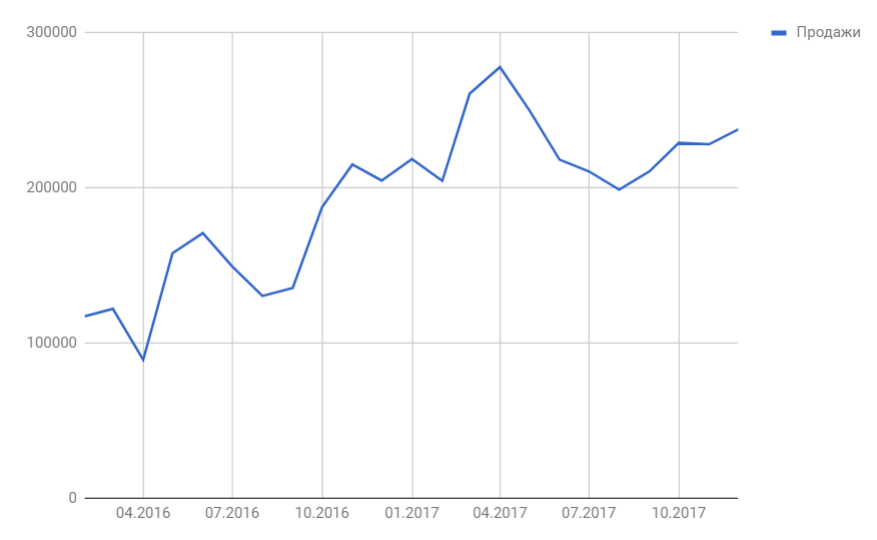
Шаг 1

Следуя нашему алгоритму, мы должны сгладить временной ряд. Воспользуемся методом скользящей средней. Видим, что в каждом году есть большие пики (май-июнь 2016 и апрель 2017), поэтому возьмем период сглаживания пошире, например, месячную динамику, т.е. 12 месяцев.

Удобнее брать период сглаживания в виде нечетного числа, тогда формула для расчета уровней сглаженного ряда:

yi — фактическое значение i-го уровня ряда,

yt — значение скользящей средней в момент времени t,

2p+1 — длина интервала сглаживания.

Но так как мы решили использовать месячную динамику в виде четного числа 12, то данная формула нам не подойдет и мы воспользуемся этой:

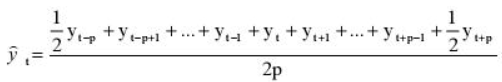
Иными словами, мы учитываем половины от крайних уровней ряда в диапазоне, в остальном формула не претерпела больше никаких изменений. Вот ее точный вид для нашей задачи:

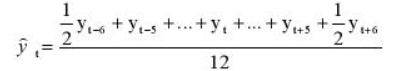
Сглаживаем наши уровни ряда и растягиваем формулу вниз:

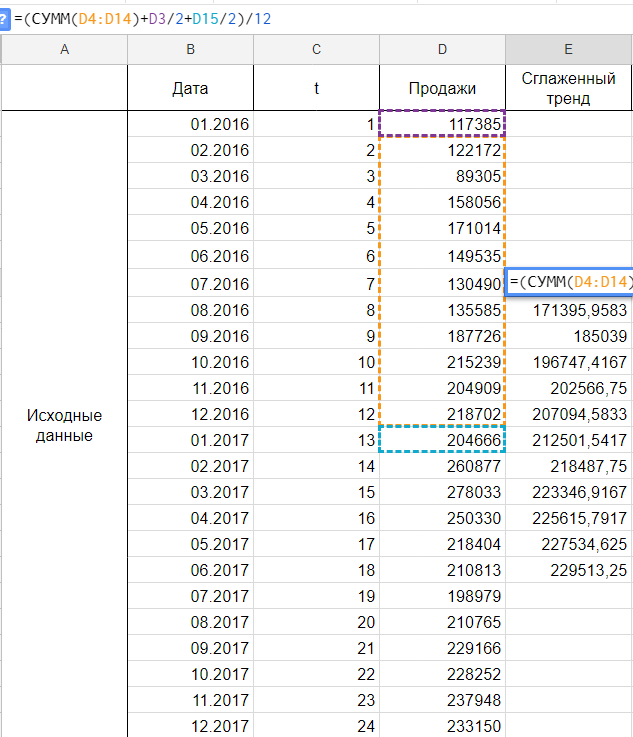
Сразу можем построить график из известных значений уровня продаж и их сглаженной. Выведем ее уравнение и значение коэффициента детерминации R^2:

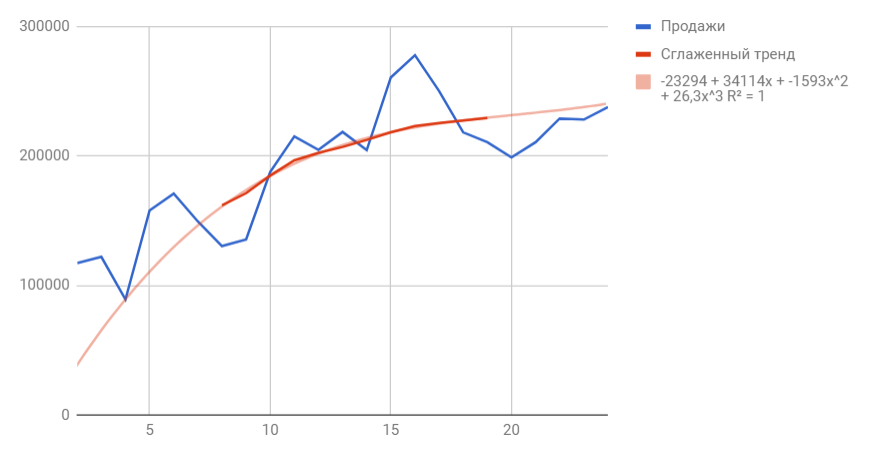
В качестве сглаженной я выбрала полином третьей степени, так как он лучше всего описывал уровни временного ряда и имел наибольший R^2.

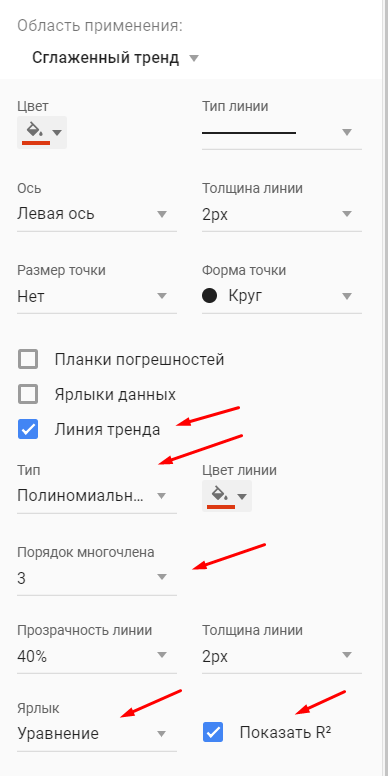
Шаг 2

Так как мы рассматриваем аддитивную модель вида: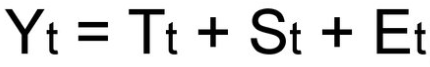

Найдем оценки сезонной компоненты как разность между фактическими уровнями ряда и значениями скользящей средней St+Et = Yt-Tt, так как Yt и Tt мы уже знаем.

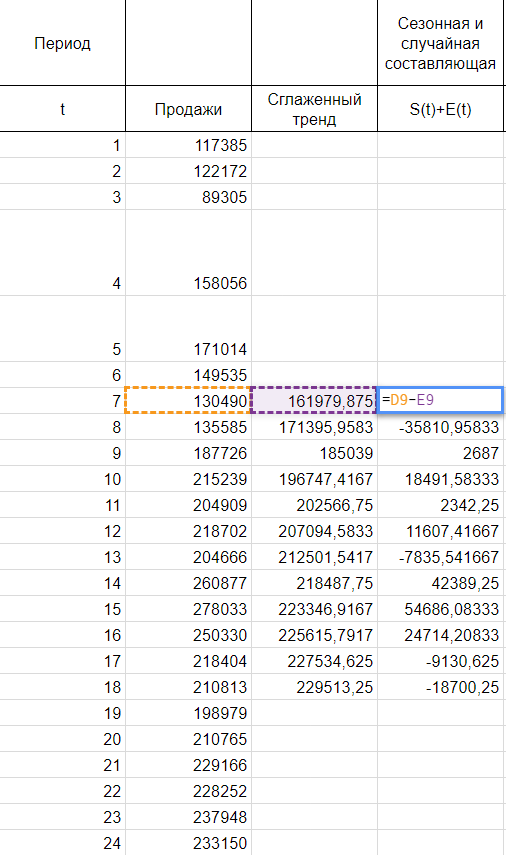
Используем оценки сезонной компоненты (St+Et) для расчета значений сезонной компоненты St. Для этого найдем средние за каждый интервал (по всем годам) оценки сезонной компоненты St.

Средняя оценка сезонной компоненты находится как сумма по столбцу, деленная на количество заполненных строк в этом столбце. В нашем случае оценки сезонной составляющей расположились в строках без пересечений, поэтому сумма по столбцам состоит из одиночных значений, следовательно и среднее будет таким же. Если бы мы располагали периодом побольше, например с 2015, у нас бы добавилась еще одна строка и мы смогли бы полноценно найти среднее, поделив сумму на 2.

В моделях с сезонной компонентой обычно предполагается, что сезонные воздействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем интервалам должна быть равна нулю. Поэтому найдя значение случайной составляющей, поделив сумму средних оценок сезонной составляющей на 12, мы вычитаем ее значение из каждой средней оценки и получаем скорректированную сезонную компоненту, St.

Далее, заполняем нашу таблицу значениями сезонной составляющей дублируя ряд каждые 12 месяцев, то есть три раза:

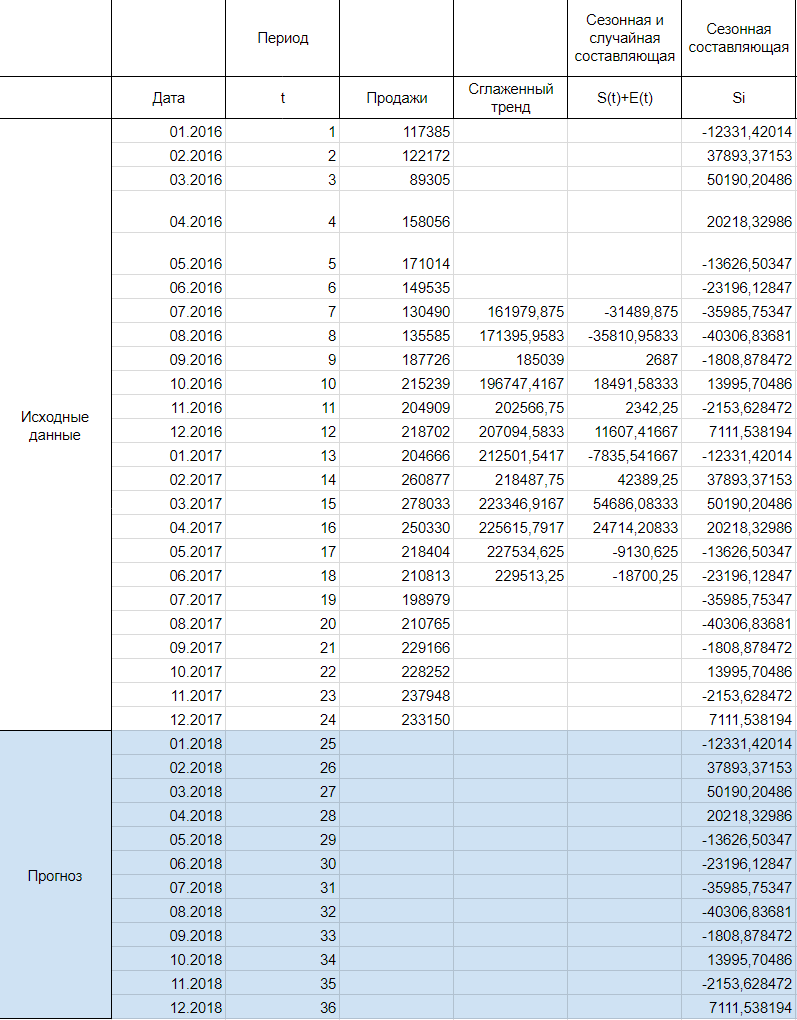
Шаг 3

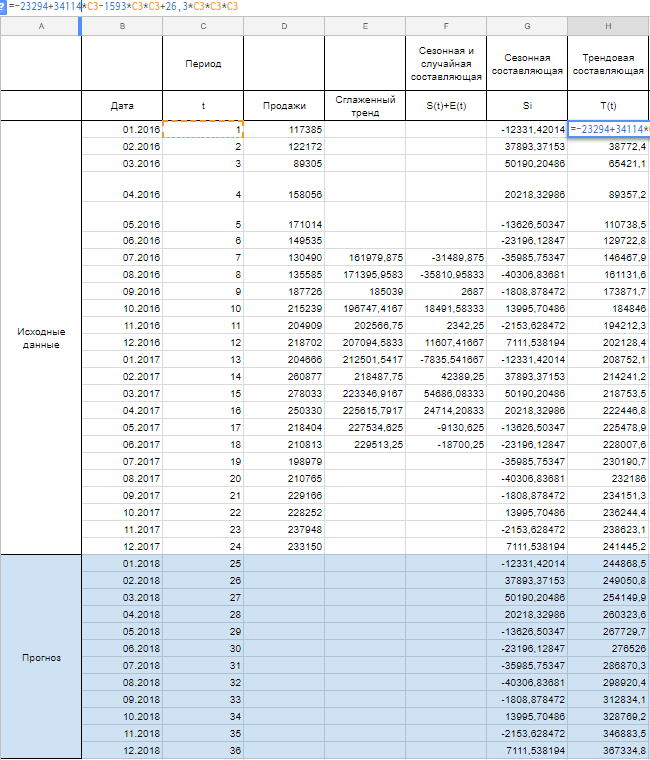
Теперь рассчитываем значения уровня тренда T(t) по тому уравнению, которое мы получили при построении сглаженного тренда на первом шаге.

T(t) = — 23294 + 34114 * t — 1593 *t^2 + 26,3 *t^3

Вместо t используем значения из столбца Период из соответствующей строки.

Шаг 4

Имея рассчитанные значения S(t) и T(t) мы можем рассчитать прогнозные значения уровней ряда Y(t). Для этого накладываем уровни сезонности на тренд.

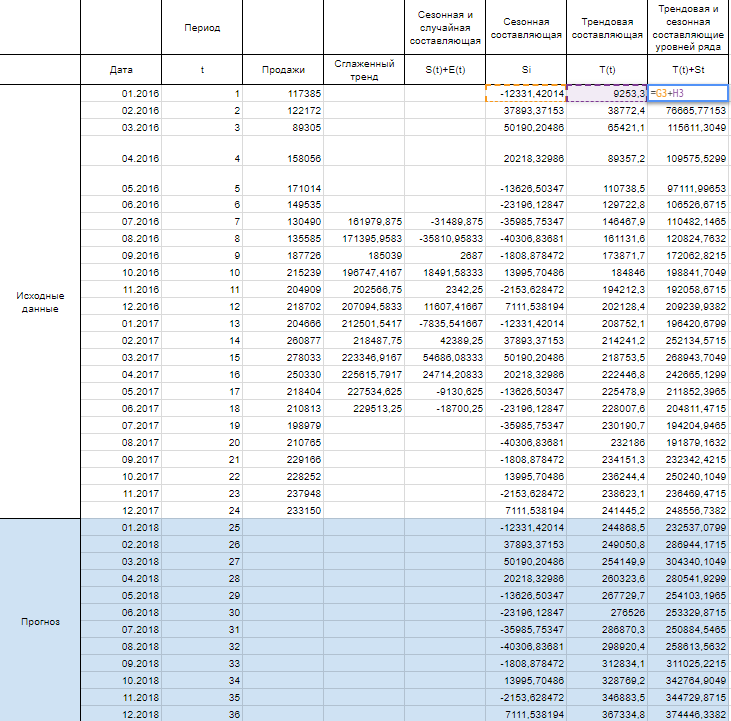
Теперь построим график известных значений Y(t) и спрогнозированных за 2018 год.

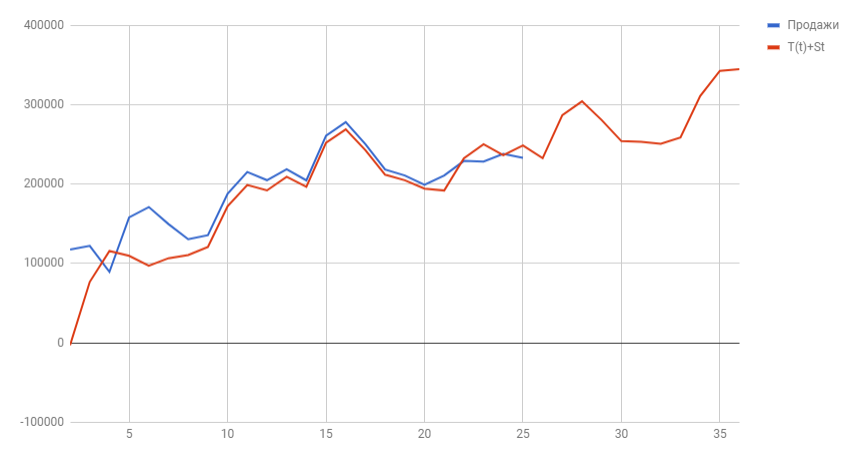
Вот мы и нашли спрогнозированные значения уровней продаж на 2018 год. Значения отражают возрастающую тенденцию и сезонные пики. Конечно, эти данные не дают 100% точности, ведь существует множество внешних воздействий, которые могут изменить направление тренда, поэтому к прогнозным значениям обычно строят доверительный интервал, это такой коридор, внутри которого могут колебаться прогнозные значения с заданной вероятностью (чаще всего выбирают 95%). Но об этом я расскажу в следующей статье.

Шаг 5

Осталось оценить точность модели. Для этого будем использовать среднюю ошибку аппроксимации, которая поможет рассчитать ошибку в относительном выражении. Иными словами, это среднее отклонение расчетных значений от фактических, которое вычисляется по формуле:

yi — спрогнозированные уровни ряда,

yi* — фактические уровни ряда,

n — количество складываемых элементов.

Модель может считаться адекватной, если:

Итак, рассчитываем ошибку аппроксимации для нашего случая. Так как в основе нашего тренда лежит полином третьей степени, прогнозные значения начинают хорошо повторять фактические значения к концу 2016 года, думаю, я думаю, поэтому корректнее было бы рассчитать ошибку аппроксимации для значений 2017 года.

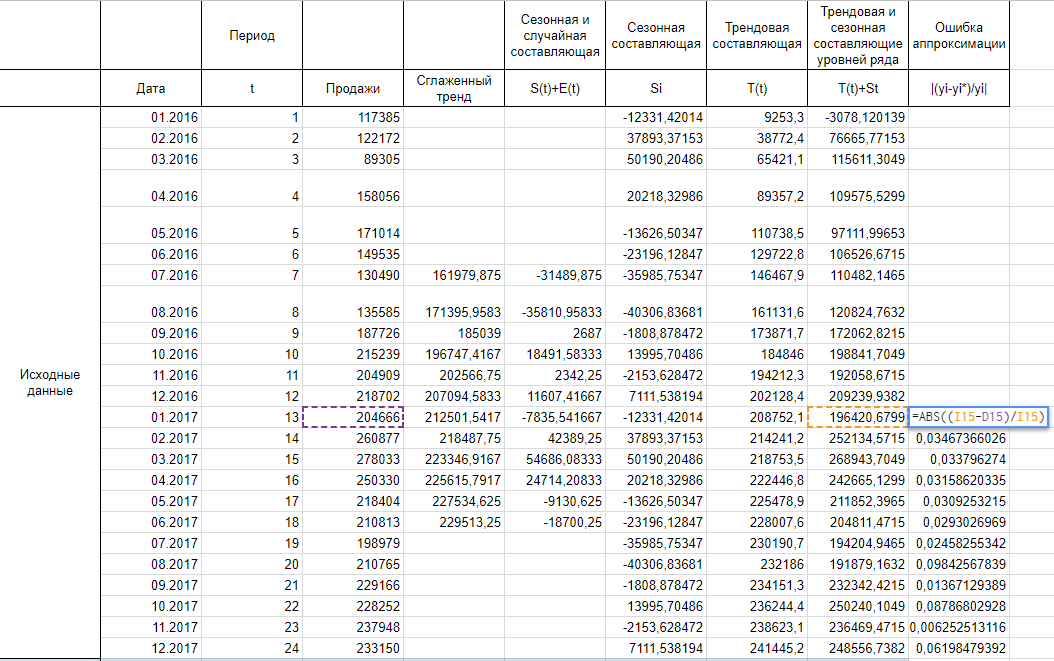
Сложив весь столбец с ошибками аппроксимации и поделив на 12, получаем среднюю ошибку аппроксимации 4,13%. Это значение меньше 15% и можем сделать вывод об адекватности модели.

Не забывайте, что прогнозы не бывают точными на 100%. Любые неожиданные внешние воздействия могут развернуть значения уровней ряда в неизвестном направлении

Лабораторная работа по EXCEL — ГРАФИЧЕСКОЕ ИЗОБРАЖЕНИЕ СТАТИСТИЧЕСКИХ ДАННЫХ И ПРОГНОЗИРОВАНИЕ В

Как организовать дистанционное обучение во время карантина?

Помогает проект «Инфоурок»

ГРАФИЧЕСКОЕ ИЗОБРАЖЕНИЕ СТАТИСТИЧЕСКИХ ДАННЫХ И ПРОГНОЗИРОВАНИЕ В ЭЛЕКТРОННЫХ ТАБЛИЦАХ.

Цель занятия. Изучение информационной технологии использования возможностей Excel для статистических расчетов, графического представления данных и прогнозирования.
Инструментарий. ПЭВМ IBM PC, программа MS Excel.

Литература.
1. Информационные технологии в профессиональной деятельности : учебное пособие/ Елена Викторовна Михеева. – М.: Образовательно-издательский центр «Академия», 2004.

Задание 1. С помощью диаграммы (обычная гистограмма) отобразить данные о численности населения России (млн. чел.) за 1970- 2005 гг.

Исходные данные представлены на рис.1, результаты работы на рис.3

Рис.1.

1. Откройте редактор электронных таблиц Microsoft Excel и создайте новую электронную книгу (при стандартной установке MS Office выполните Пуск/Все программы/ Microsoft Excel ).

2. Создайте на листе 1 таблицу численности населения по образцу (рис.1). Для ввода значений лет создайте ряд чисел с интервалом в 7 лет (введите первые два значения даты — 1970 и 1977, выделите обе ячейки и протяните вправо за маркер автозаполнения до нужной конечной даты).

3. Постройте диаграмму (обычная гистограмма) по данным таблицы. Для этого выделите интервал ячеек с данными численности населения А3:G3 и выберите команду Вставка/Диаграмма . На первом шаге работы с Мастером диаграмм выберите тип диаграммы – гистограмма обычная; на втором шаге на вкладке Ряд в окошке Подписи оси Х укажите интервал ячеек с годами В2: G2 (рис.2). Далее введите название диаграммы и подписи осей; дальнейшие шаги построения диаграммы осуществляется по подсказкам мастера.

Рис.2.

Задание 2. Осуществить прогноз численности населения России на 2012 г. добавлением линии тренда к ряду данных графика.

Краткая справка. Для наглядного показа тенденции изменения некоторой переменной целесообразно на график вывести линию тренда. Это возможно не для всех типов диаграмм, а только для гистограмм, линейчатых диаграмм, диаграмм с областями, графиков. Введенная линия тренда сохраняет связь с исходным рядом, т.е. при изменении данных соответственно изменяется линия тренда. Линию тренда можно использовать для прогноза данных.

1. Добавьте линию тренда к диаграмме, построенной в Задании 1. Для этого сделайте диаграмму активной щелком мыши по ней и в меню Диаграмма выберите команду Добавить линию тренда.

2. В открывшемся окне Линия тренда (рис.3) на вкладке Тип выберите вид тренда полиномиальный 4-й степени;

Рис.3

3. Для осуществления прогноза на вкладке Параметры введите название кривой «Линия тренда» и установите параметр прогноза — вперед на один период (рис.4).

Рис.4

4. На диаграмме будет показана линия тренда и прогноз на один период вперед (рис.5).

5. Добавьте линии сетки на диаграмме ( Диаграмма/ Параметры диаграммы/ Линии сетки ).

Измените цену одного деления оси Y с 5 на 1 (Выполните двойной щелчок по оси и на вкладке «Шкала» задайте новые значения).

Средствами рисования проведите линию красного цвета (на ось Y) для определения значения прогноза на 2012 г.

Если вы все сделали правильно, то прогноз численности населения России по линии тренда составит 131 млн.чел.

Внесите численное значение прогноза на 2012 г. в исходную таблицу.

Задание 3. Построить график о числе заключенных браков населением России. Добавить линейную линию тренда и составить прогноз на три периода вперед.

Исходные данные представлены на рис. 6, результаты работы на рис. 7.

Рис. 6

Рис. 7